| Up: |
|
A Fast and Accurate Light Reflection Model |
| Previous: |
|
Introduction |
| Next: |
|
Physical Parameters |
The geometry of light reflection at a surface is illustrated in Figure 2. The polar and azimuthal angles of incidence and reflection are given by (θi,φi) and (θr,φr), respectively, and the solid angle of the incident light is given by dωi. The polar angles are measured from the surface normal. For isotropic surfaces, the BRDF is independent of φi because of rotational symmetry.
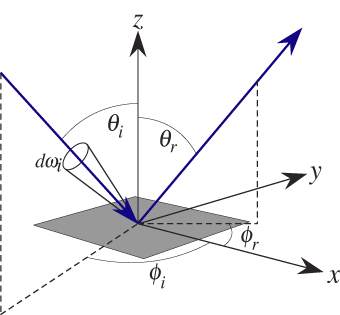
Figure 2: Geometry of incident and reflected light
We can express the incident energy flux dEi in terms of the incident radiance Ii, the incident angle θi and the incident solid angle dθi
| dEi = Ii • cosθi • dωi | (2) |
| Converted to HTML by Stephen H. Westin <swestin@earthlink.net> Last modified: Mon Sep 5 22:07:26 EDT 2011 |