| Up: |
|
Components of the BRDF |
| Previous: |
|
Components of the BRDF |
| Next: |
|
Directional diffuse component |
The specular component is responsible for sharp mirror-like reflection from a surface. It can be expressed as a product:
| dIr,sp = |F|2 • e-g • S • Ii | (5) |
where |F|2 is the Fresnel reflectivity, which is a function of the incidence angle and the refractive index n of the material, g is a function of the surface roughness, and S is a geometrical shadowing function.
The following interactive display illustrates how the Fresnel term |F|2 varies with θi and n. The incidence angle θi is evaluated at the center of the incident light cone on the left. The length of the cone of reflection on the right is proportional to the magnitude of |F|2. The solid-line semicircle is of unit radius and is included for reference.
Figure 6: Interactive display of Fresnel term
|F|2. Double click the figure to activate the
control panel; click “Play” to activate a
demonstration.
The function g, which depends on the effective surface roughness σ, is given by:
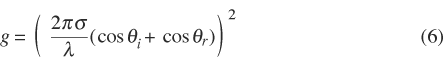
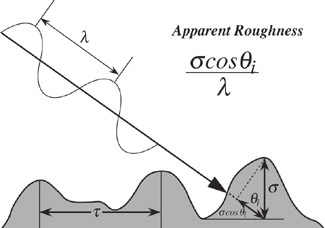
Figure 7: Schematic of rough surface and incident light wave
The interactive figure below illustrates how the exponential e-g varies with θi, σ, τ and τ. The effective roughness σ is generally smaller than the root-mean-square vertical surface roughness height σ0 due to shadowing effects. Although σ is a function of θi, θr, τ, and σ0, it is found that σ depends primarily on σ0 [HE91]. For this reason, σ0 is the parameter varied on the “sigma” slider of the control panels. The τ-dependence of e-g arises from the secondary dependence of the effective roughness σ on τ. In Figure 8, the solid-line semicircle is the unit hemisphere. The length of the cone of reflection is proportional to e-g. A statistically-generated Gaussian rough surface topography is shown schematically, with the vertical scale amplified with respect to the horizontal (by about a factor of ten).
Figure 8: Interactive display of
e-g term. Double click the figure to activate.
The shadowing term S is illustrated below. It varies with σ0 and τ. The solid-line semicircle is the unit hemisphere, representing the limit of no shadowing. The function S is defined in [HE91].
Figure 9: Interactive display of shadowing term S
Finally, let's see how the entire specular component dIr,sp varies with the parameters θi, σ, τ, λ material. The length of the cone of reflection on the right side in Figure 10 is proportional to dIr,sp. The solid-line semicircle has a radius equal to the incident radiance, Ii. This limit is achieved for ideal-specular, 100% reflection of the incident beam.
Figure 10: Interactive display of entire specular term
| Up: |
|
Components of the BRDF |
| Previous: |
|
Components of the BRDF |
| Next: |
|
Directional diffuse component |
| Converted to HTML by Stephen H. Westin <swestin@earthlink.net> Last modified: Mon Sep 5 22:26:23 EDT 2011 | This document is not valid HTML. Look here to learn why. |